| V I S U A L I Z Z A D I S C U S S I O N E |
| Domenicodattoma |
Inserito il - 04/02/2010 : 12:46:48
Ragazzi vorrei sapere come si riconosce un reticolo dstributivo? Il riconoscimento è grafico o si effettuano delle operazioni? Grazie mille! |
| 20 U L T I M E R I S P O S T E (in alto le più recenti) |
| batonin |
Inserito il - 31/10/2012 : 12:25:09
Dovrebbe essere distributivo perche non ci sono elementi con piu complementi e nessun sottoreticolo di tipo m3 o n5, giusto? |
| batonin |
Inserito il - 30/10/2012 : 19:06:05
Ah ok grazie mille per la disponibilita.
Ma quindi questo reticolo è distributivo o no? |
| marilenadn |
Inserito il - 30/10/2012 : 18:31:41
Si, è limitato. Non è complementato perchè b non ha complemento.
Ma attenzione perchè non è corretto dire che NON è distributivo perchè non esistono elementi che hanno più complementi. E' corretto dire che non è distributivo perchè ci sono elementi con più complementi. |
| batonin |
Inserito il - 30/10/2012 : 16:49:33
Si infatti...e diventa un cubo poi (mettendo e ed f sopra c ed d).
Se non erro, il reticolo è limitato da a ed g, non è complementato perche non tutti gli elementi hanno complemento (in questo caso credo che solo b non abbia complemento) e non è distribuito perche non c'è nessun elemento con piu di un complemento e nessun sottoreticolo del tipo M3 o N5: giusto? |
| marilenadn |
Inserito il - 30/10/2012 : 16:36:50
Aggiungerei una linea che collega "b" con "e" e "b" con "f" |
| batonin |
Inserito il - 30/10/2012 : 15:39:52
Grazie mille, davvero ;-) |
| marcospider |
Inserito il - 30/10/2012 : 08:31:28
![]()
Immagine:
17,48 KB
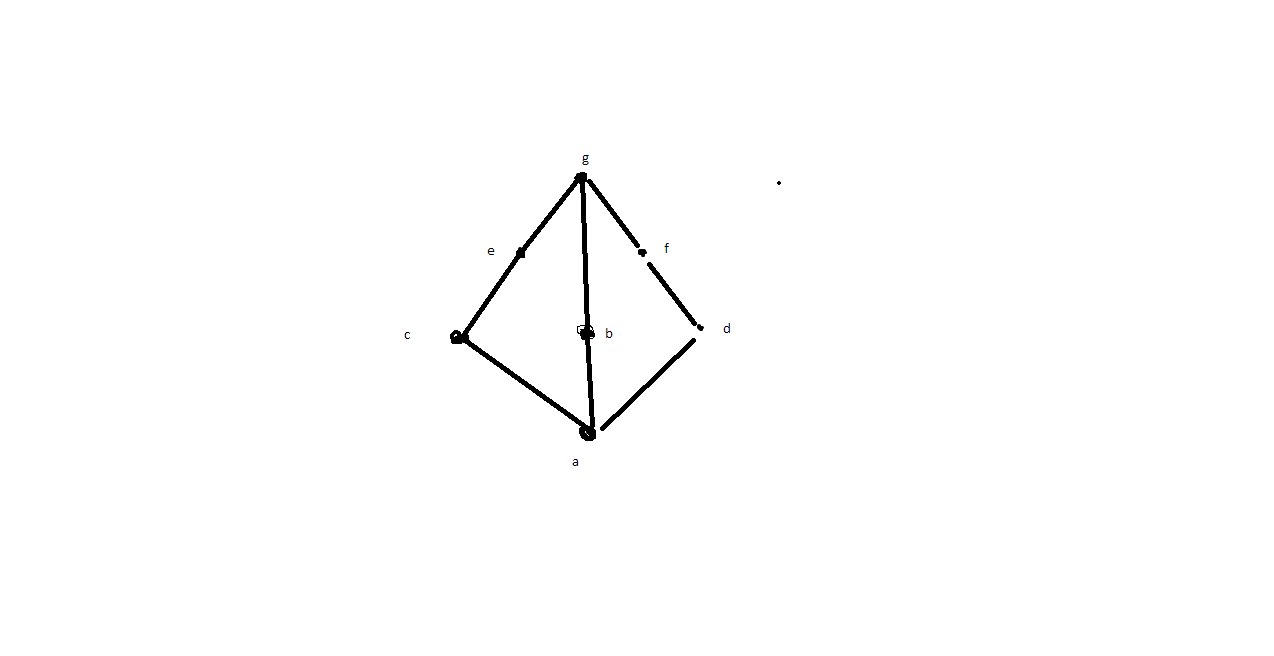
dovrebbe essere così il grafico (anche se non molto curato XD)
ho cercato di ricordarmi qualcosa di discreta |
| batonin |
Inserito il - 24/10/2012 : 12:22:11
Nessuno mi aiuta :( |
| batonin |
Inserito il - 18/10/2012 : 08:20:18
Ah giusto stewie, hai ragione non me n'ero accorto :D
Gentilmente potresti dirmi com'è il grafico dell'ultimo mio post in modo da chiarirmi gli ultimi dubbi sui reticoli?
Sull'insieme A={a,b,c,d,e,f,g} è data la relazione d'ordine R={(x,x)|x€A} U {(a,x)|x€A} U {(x,g)|x€A} U {(c,e),(b,e),(b,f),(d,f)}
Per favore, potresti farmi capire come si fa il grafico in questo caso? Mi basterebbe anche solo il grafico...
Con questo grafico non dovrei piu darti fastidio, promesso!!!
Grazie tante ancora, buona giornata. |
| Stewie83 |
Inserito il - 17/10/2012 : 21:11:07
allora.....
Il reticolo che ti ho mostrato è Complementato.....Tutti gli elementi hanno un complemento...
Essendo mcm e MCD commutativi....non ho scritto la forma duale degli elementi...perchè ovvia...
Per fartelo capire nuovamente...TUTTI I COMPLEMENTI sono:
1-->70
2-->35
5-->14
7-->10
10-->7
14-->5
35-->2
70-->1 |
| batonin |
Inserito il - 17/10/2012 : 17:17:38
Stewie, un ultimo aiuto per favore....Credo di aver capito i reticoli quando sono presenti numeri interi, ora il mio problema sorge davanti a tracce con relazioni!!! Ti faccio un esempio, sperando che tu possa essere per un ulteriore volta talmente gentile da spiegarmi come si fa il diagramma di Hasse:
Sull'insieme A={a,b,c,d,e,f,g} è data la relazione d'ordine R={(x,x)|x€A} U {(a,x)|x€A} U {(x,g)|x€A} U {(c,e),(b,e),(b,f),(d,f)}
Per favore, potresti farmi capire come si fa il grafico in questo caso? Mi basterebbe anche solo il grafico...
Grazie mille ancora una volta anticipatamente, anche a nome di chi come me sta capendo i reticoli grazie al tuo aiuto ;-) |
| batonin |
Inserito il - 17/10/2012 : 12:48:36
Grazie ancora stewie, ora dovrebbe essere tutto chiaro ;-)
Se non erro quindi, il reticolo non è di Boole perchè non è complementato (non tutti gli elementi hanno un complemento) e il reticolo dei divisori di 14 è un sottoreticolo (è la base del cubo dell'immagine): giusto?
Grazie ancora per la pazienza e disponibilità, buona giornata. |
| Stewie83 |
Inserito il - 16/10/2012 : 21:44:39
Noto a priori che hai troppe lacune in merito a Discreta.....
Inizio per dirti che se hai preso bene appunti....e te lo sta dicendo uno che ancora deve sostenere questo esame non per ignoranza ma perchè non ha mai voglia di studiare....devi fare attenzione ai minimi particolari senza scrivere le cose come sono scritti negli appunti.....
Al momento non ho nessun appunti sotto mano...causa prestito.....cmq....se non ricordo male e ti rinfresco le idee....i complementi di un elemento di un reticolo è di una banalità ancor più banale del disegno.....Tralasciando questa premessa...ti dico già che il grafico diventa la soluzione di qualunque quesito...
Se noti bene...dal mio grafico capirai che i vari complementi sono questi:
2-35
5-14
7-10
1-70 (banalmente)
Tradotto in formule
1) (x ^ x’=0) ------------>MCD
2)(x v x’=1). ------------>mcm
Se rileggi i tuoi appunti....la 1) e la 2) non sono altro che MCD(x1,x2)=1 mcm(x1,x2)=70
MCD(2,35)=1 ^ mcm(2,35)=70
MCD(5,14)=1 ^ mcm(5,14)=70
MCD(7,10)=1 ^ mcm(7,10)=70
MCD(1,70)=1 ^ mcm(1,70)=70
Anche gli altri quesiti sono di una facilità mostruosa....ma te li lascio per compitino.... |
| batonin |
Inserito il - 16/10/2012 : 12:40:53
Grazie mille Stewie83 per aver inserito l'immagine, hai chiarito i miei dubbi: grazie mille!!! ;-)
Saresti cosi gentile da rispondere alle domande presenti sulla traccia di questo esercizio, in modo da farmi capire definitivamente come si ragiona sui reticoli? Magari anche spiegando brevemente come si ragiona...
Le domande sono le seguenti:
a) determinare, se esistono, i complementi di ciascun elemento
b) stabilire se si tratta di un reticolo di Boole
c) verificare se il reticolo dei divisori di 14 è un suo sottoreticolo.
Io ho le seguenti definizioni ma non riesco ad applicarle all'esercizio in questione:
Complemento: se in un reticolo limitato (cioè ammette minimo e massimo) esiste x’ in A t.c.: (x ^ x’=0) ^ (x v x’=1).
Reticolo di Boole: quando un reticolo è distributivo e complementato (quindi anche limitato).
Sottoreticolo: quando, per ogni x,y € B, sia l’estremo inferiore di {x, y} sia l’estremo superiore di {x, y} appartengono a B (con (A, #8804;) un reticolo e B sottoinsieme di A).
Distributivo: Consideriamo un reticolo (A, #8804;) esso si dirà DISTRIBUTIVO se sono verificate le proprietà per ogni x,y,z € A:
1) x v (y ^ z) #8804; (x v y) ^ (x v z)
2) x ^ (y v z) #8805; (x ^ y) v (x ^ z)
|
| Stewie83 |
Inserito il - 14/10/2012 : 19:29:57
facilissimooo
Immagine:
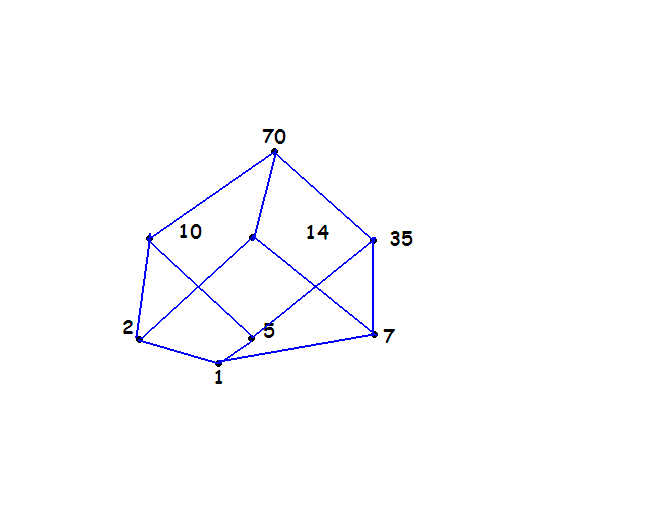
11,71 KB |
| batonin |
Inserito il - 10/10/2012 : 11:08:24
Ragazzi, sareste cosi gentili da spiegarmi in che modo si uniscono i punti di un diagramma di Hasse?
Ad esempio, ho A={n€N | n divide sia 210 che 140}. Mi trovo il MCD(210,140)= 70 e quindi considero un nuovo insieme composto dai divisori di 70: questo insieme sarà quindi A={1,2,5,7,10,14,35,70}.
Giusto?
Ovviamente gli apici del diagramma di Hasse saranno 1 e 70, rispettivamente minimo e massimo. Ma gli altri punti in che modo li unisco? Cioe, con quale ragionamento?
Grazie mille a tutti coloro che vorranno aiutarmi, buona giornata. |
| rem |
Inserito il - 13/06/2011 : 20:39:29
ragazzi come faccio a mostrare che i reticoli N5 e M3 non sono distributivi? |
| bantux87 |
Inserito il - 05/02/2010 : 18:46:03
si vedendo i complementi nn perdi tempo a cercare sottoreticoli a meno ke non te lo kieda la traccia..ma di solito nn dovrebbe kiederlo |
| Domenicodattoma |
Inserito il - 05/02/2010 : 18:21:25
Si si, l'insieme è quello, e in effetti Gogeta ha ragione...evidentemente la prof si sarà sbagliata...comunque trovo più comodo farlo con la regola dei complementi...speriamo bene! :D
Grazie ad entrambi per l'aiuto!!!! |
| bantux87 |
Inserito il - 05/02/2010 : 17:34:02
il reticolo non è distributivo..come diceva gogeta nn vale una delle due proprietà distributive..xò la prof disse un reticolo non distributivo contiene necessariamente un sottoreticolo di tipo M3 o N5..che ineffetti sembra nn esserci..perkè se togli il 6 dall'insieme hai che mcm(3,4)=12 ke nn appartiene all'insieme ke ci hai dato..se togli invece il 3 il MCD(6,8)=2 che nn appartiene all'insieme..nn si riesce a far valere la chiusura..sicuro ke è quello l'insieme?è strano.. |
|
|


