| V I S U A L I Z Z A D I S C U S S I O N E |
| JediKnight |
Inserito il - 15/02/2005 : 12:15:00
allora, l'esercizio del sottogruppo di Z[11]* è un banale esercizio sugli omomorfismi,
l'ho risolto ma è impossibile scrivere qui tutti i passaggi.
brevemente: poichè il generatore del sottogruppo è 4 e gli elementi appartengono a Z[11]
H=[ 1, 4, 5, 9, 3]
Il periodo di 4 è 5, dato che 4 elevato a 5 è cogruo a 1 mod 11, cioè dà l'el neutro
gli altri periodi si trovano con la formula a^k=n/(MCD n,k) poichè ogni elemento è in funzione di 4
1 ha periodo 1, gli altri tutti 5
Poichè ogni elemento è determinato da 4 ed è f:(H,*)->(H,*),
nell'omomorfismo f(x)=f(4^k)=f(4)^k
poichè |f(4)| deve dividere MCD ( |4|,|H|), abbiamo che |f(4)| divide 5 e allora le possibilità
sono che f(4)=1,5,9,3 (sono classi di equivalenza) poichè i loro periodi dividono 5
se f(4)=1 si ha l'omomorf banale
se f(4)=5 allora f(1)=f(4^5)=f(4)^5= 5^5= 1 (sono classi di equivalenza)
così via, si ha f(5)=3 , f(9)=4, f(3)=9
Poichè f trasforma il generatore di H nel generatore di H essendo f:H->H, e cioè f(x) ci
ha dato tutto H, l'omomorfismo è bigettivo, cioè ISOMORFISMO
anche nel caso f(4)=9 ed f(4)=3 si hanno isomorfismi
Per l'esercizio sull'anello, io ho inteso in questo modo:
Poichè (a+1)^2=0, si deve avere che a+1=0 intendendo che A è un insieme di classi di
equivalenza, tipo Z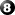 , ecc.... , ecc....
così facendo, abbiamo che a è una classe di equivalenza, e a+1= 0 (mod n) (congruenza
con n l'indice di A )
se a+1= 0 (mod n), allora anche -(a+1)=0 (mod n) e cioè
-a=1 (mod n)
e cioè MCD(n,-a) è 1 (ricordando che a è una classe di eq) e quindi a appartiene al gruppo
degli elementi unitari di A, dato che ha inverso
Interpretandolo in Z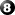 , abbiamo che U(Z8)=[1,3,5,7] , abbiamo che U(Z8)=[1,3,5,7]
se prendiamo la classe 7, abbiamo che 7+1=0 e -a=-7 è congruo 1 che appartiene a U(Z8)
prendiamo 15, 15+1=16=0 abbiamo -a=-15 che è sempre 1, che è sempre appartenente a U(Z8)
|
| 10 U L T I M E R I S P O S T E (in alto le più recenti) |
| JediKnight |
Inserito il - 17/02/2005 : 20:17:40
Citazione:
Messaggio inserito da Arpino
secondo me l'esercizio sugli anelli è sbagliato:
l'esercizio chiede di provare che -a ha inverso quindi bisogna trovare un x appartenente ad A tale che -a*x = 1.
(a+1)^2 = 0 <=> a^2+1+2a=0 mettendo in evidenza la a avremo che
a(a+2)+1=0 <=> a(a+2) =-1, moltiplicando tutto per -1 si ha
-a(a+2) = 1 e quindi x = a+2 ed è l'inverso di -a.
credo tu abbia ragione, vabè, tieni presente che io me lo sono inventato in 10 minuti, inoltre ho già dato...  
|
| francesca |
Inserito il - 16/02/2005 : 17:23:07
Qui trovi l'appello del 15, ma e' del corso B http://www.laureateci.it/forum/topic.asp?TOPIC_ID=2831
Il corso A lo ha fatto il 14, ma non ho la traccia 
|
| alexia |
Inserito il - 16/02/2005 : 15:40:29
Qualcuno ha per caso la traccia dell'appello del 15 del corso A? grazie
|
| Arpino |
Inserito il - 15/02/2005 : 23:37:29
non credo che metteranno un appello starordinario a Marzo. lo ha detto anche Visaggio: "Non ci sono i presupposti"... che cavolo volesse dire non lo so però ha detto così |
| francesca |
Inserito il - 15/02/2005 : 21:38:39
I risultati escono giovedi...e SECONDO REGOLAMENTO devono fare l'orale entro venerdi! Vedremo!
Perchè se l'orale non si riesce a fare, coincidera' con le lezioni...quindi...non si spiegherebbe poi un rifiuto dell'appello straordinario a marzo!Vedremo |
| Arpino |
Inserito il - 15/02/2005 : 21:05:16
secondo me l'esercizio sugli anelli è sbagliato:
l'esercizio chiede di provare che -a ha inverso quindi bisogna trovare un x appartenente ad A tale che -a*x = 1.
(a+1)^2 = 0 <=> a^2+1+2a=0 mettendo in evidenza la a avremo che
a(a+2)+1=0 <=> a(a+2) =-1, moltiplicando tutto per -1 si ha
-a(a+2) = 1 e quindi x = a+2 ed è l'inverso di -a. |
| JediKnight |
Inserito il - 15/02/2005 : 19:15:36
Citazione:
Messaggio inserito da bull3t
Un grazie infito JediKnight ; ora me li studio ben bene sperando che l'orale, se lo scritto è passato, si focalizzi su questi due esercizi che non ho risolto 
ciao
agli orali a cui ho assistito,gli esercizi del compito neanche li hanno nominati |
| JediKnight |
Inserito il - 15/02/2005 : 19:14:01
Ma i risultati degli scritti sono già usciti? possibile? |
| bull3t |
Inserito il - 15/02/2005 : 13:53:54
Qualcuno sa se l'orale si terrà giovedì o un altro giorno? |
| bull3t |
Inserito il - 15/02/2005 : 12:36:42
Un grazie infito JediKnight ; ora me li studio ben bene sperando che l'orale, se lo scritto è passato, si focalizzi su questi due esercizi che non ho risolto 
ciao |
|
|




