| V I S U A L I Z Z A D I S C U S S I O N E |
| Joseph88 |
Inserito il - 20/04/2010 : 12:32:08
Esercizio 4
Siano X una V.A. N(#8722;1, 1), Y e Z due V.A. N(0, 9) indipendenti.
• Calcolare E[1 #8722; (X #8722; 2Y )^2] e V ar(#8722;3X + Y + 2).
• Costruire a partire da X, Y e Z una V.A. di Student con 2 gradi di liberta’.
Come avete risolto questo esercizio??? 
Vi ringrazio in anticipo!!!  |
| 15 U L T I M E R I S P O S T E (in alto le più recenti) |
| Spidey |
Inserito il - 19/06/2010 : 20:07:52
Citazione:
Messaggio inserito da Masterkoala
Mi spiegate i singoli passaggi per il calcolo della varianza?
Ciao Masterkoala, i singoli passaggi per il calcolo della varianza sono questi:
Var(-3X + Y - 2) = Var(-3X) + Var(Y) + Var(-2) = [(-3)^2]*Var(X) + Var(Y) + 0 = 9*Var(X) + Var(Y) = 9*1 + 9 = 18
Citazione:
Messaggio inserito da Masterkoala
[...]Che proprietà utilizzate?
Inutile dire che le proprietà utilizzate sono quelle scritte sugli appunti del corso, precisamente al giorno 17 Marzo 2010. Si tratta di cinque proprietà semplici semplici che troverai sui tuoi appunti sotto la dicitura "Proprietà di Var(X)"  Buona fortuna! Buona fortuna!
Ciao ciao. |
| Masterkoala |
Inserito il - 19/06/2010 : 00:59:39
Mi spiegate i singoli passaggi per il calcolo della varianza?
Che proprietà utilizzate?
Grazie.... |
| Mk178 |
Inserito il - 22/04/2010 : 21:50:58
certo ke può essere negativo!... è la varianza ke deve essere > 0...
es.
X | Px
2 | 0,3
1 | 0,2
-3 | 0,5
E[X]= 2*0,3 + 1*0,2 + (-3)*0,5 = 0,6 + 0,2 - 1,5 = -0,7
O molto più banalmente, come dice joseph, ci sono molti esempi di gaussiane negli esercizi, con mu negativo...(La stessa X~N(-1, 1) di questo esercizio) ;P
|
| Joseph88 |
Inserito il - 22/04/2010 : 19:20:08
Ihihihihih!!! Hai ragione! :D
Comunque hai chiesto quella cosa al docente?
Comunque penso sia possibile che il valore atteso sia negativo:
in un esercizio con V.A. normale avevamo come valori (-1,1),
quindi penso che il valore atteso possa essere negativo! |
| Spidey |
Inserito il - 22/04/2010 : 12:54:11
Citazione:
Messaggio inserito da Joseph88
Caro Spidey,
hai sbagliato, perché al punto primo abbiamo:
E[1 -(X - 2Y)^2] = 1 -(E[X^2] +4*E[Y^2] -4*E[X]*E[Y])=
=1 -E[X^2] -4*E[Y^2] +4*E[X]*E[Y] = -37
Ciao a tutti, in effetti rifacendo i conti, ho fatto un errore ed ho fatto un macello col segno meno davanti al quadrato del binomio  , però mi sembra strano avere un valore atteso negativo... Boh! Potremmo chiedere al docente oggi pomeriggio. , però mi sembra strano avere un valore atteso negativo... Boh! Potremmo chiedere al docente oggi pomeriggio.
Citazione:
Messaggio inserito da Joseph88
[...] non trovo la STANDARDIZZAZIONE DI UNA V.A.,
ho trovato le V.A. di STUDENT... 
E' proprio quello l'argomento che ti serve, insieme al resto delle distribuzioni (discrete e continue).
P.S.: non mi sono arrabbiato,  ti ho solo dato il mio personalissimo parere che sei libero di tenere o no in conto e poi, se non mi facesse piacere rispondere non troveresti così tanti miei post su questo forum. ti ho solo dato il mio personalissimo parere che sei libero di tenere o no in conto e poi, se non mi facesse piacere rispondere non troveresti così tanti miei post su questo forum.
Ciao ciao. |
| FullMetal86 |
Inserito il - 21/04/2010 : 20:17:50
Si si anche a me esce -37 |
| Joseph88 |
Inserito il - 20/04/2010 : 22:48:53
Ok, grazie Mk178!
Meno male c'è qualcuno che risponde con piacere e senza arrabbiarsi!!!  |
| Mk178 |
Inserito il - 20/04/2010 : 22:11:05
Citazione:
Messaggio inserito da Joseph88
Caro Spidey,
hai sbagliato, perché al punto primo abbiamo:
E[1 -(X - 2Y)^2] = 1 -(E[X^2] +4*E[Y^2] -4*E[X]*E[Y])=
=1 -E[X^2] -4*E[Y^2] +4*E[X]*E[Y] = -37
anke a me esce -37
Citazione:
Messaggio inserito da Joseph88
Per quanto riguarda il secondo punto, sto cercando fra gli appunti,
ma non trovo la STANDARDIZZAZIONE DI UNA V.A.,
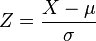
ATTENZIONE: al denominatore è sigma e non sigma quadro, quindi bisogna fare la radice della varianza! ;) |
| Joseph88 |
Inserito il - 20/04/2010 : 21:48:11
Caro Spidey,
hai sbagliato, perché al punto primo abbiamo:
E[1 -(X - 2Y)^2] = 1 -(E[X^2] +4*E[Y^2] -4*E[X]*E[Y])=
=1 -E[X^2] -4*E[Y^2] +4*E[X]*E[Y] = -37
Per quanto riguarda il secondo punto, sto cercando fra gli appunti,
ma non trovo la STANDARDIZZAZIONE DI UNA V.A.,
ho trovato le V.A. di STUDENT...  |
| Spidey |
Inserito il - 20/04/2010 : 19:34:54
Citazione:
Messaggio inserito da Joseph88
Ok... Per il primo punto i risultati coincidono!
Per il secondo punto, invece, non so da dove iniziare:
né X, né Y e né Z sono V.A. gaussiane standard,
quindi come si fa a creare una V.A. di Student?
Poi, non mi risulta che si possa trasformare
una V.A. gaussiana in una V.A. gaussiana standard!
Fare queste domande significa non aver studiato la teoria, perché altrimenti sapresti che:
- il risultato del valore atteso (al punto primo) è
E[1 - (X - 2*Y)^2] = ...(qui si applicano le proprietà del valore atteso che, appunto, si studiano)... = 1 - E[X^2] + 4*E[Y^2] - 4*E[X]*E[Y] = 35.
- il secondo punto necessita dello studio (dagli appunti o da dove vuoi tu) delle variabili aleatorie, discrete e continue, spiegate dal docente a lezione perché sapresti che la "trasformazione", come l'hai chiamata tu, è in realtà definita come standardizzazione di una v. a. e può essere effettuata nel caso dell'esercizio! 
- per quanto riguarda la creazione di una v. a. di Student, consulta i tuoi appunti al giorno 25/03/2010 e scoprirai che ciò che ti ha detto RoByY non è altro che il frutto dello studio degli appunti (o di un testo come quelli consigliati qui).
Ciao ciao. |
| RoByY |
Inserito il - 20/04/2010 : 19:29:31
Certo che si può fare. Si applica la formula (X-mu)/sigma. Avendo delle gaussiane hai anche i loro valori mu e sigma^2 e di conseguenza sigma quindi nel caso di X e Y:
(X-(-1))/1 ~ N(0,1)
(Y-0)/3 ~ N(0,1)
Per ottenere la CHI-QUADRO basta elevare al quadrato.
Se riesci leggi anche il topic sull'esercizio 10 e dimmiche ne pensi. |
| Joseph88 |
Inserito il - 20/04/2010 : 19:15:00
Ok... Per il primo punto i risultati coincidono!
Per il secondo punto, invece, non so da dove iniziare:
né X, né Y e né Z sono V.A. gaussiane standard,
quindi come si fa a creare una V.A. di Student?
Poi, non mi risulta che si possa trasformare
una V.A. gaussiana in una V.A. gaussiana standard! |
| RoByY |
Inserito il - 20/04/2010 : 18:51:29
E[1-(X-2Y)^2]= -37
Var(-3X+Y+2)= 18
T=(X+1)/sqrt((Y^2+Z^2)/(9*2)) nell'ipotesi di considerare Z come Y ed esplicitandole separatamente.
T=(X+1)/sqrt(2(Y^2)/(9*2)) nell'ipotesi di considerare Z esattamente uguale a Y.
Chiedo conferma a chiunque abbia svolto l'esercizio siccome ho anch'io qualche perplessità su questo punto. |
| Joseph88 |
Inserito il - 20/04/2010 : 18:24:59
Metteresti anche i risultati... perché in questo modo comprendo poco!  |
| RoByY |
Inserito il - 20/04/2010 : 17:58:19
Io ho risolto in questo modo.
Per quanto riguarda il valor medio hosviluppato il quadrato, scomposto il tutto nella somma di valori medi e calcolando il valore.
Stessa cosa per la varianza: scomposizione e somma di valori.
Nell'ultimo quesito, per creare una VA di Student occorre che X sia GAUSSIANA STANDARD e Y una CHI-QUADRO con n gradi di libertà.
Siccome ho notato che Z è come Y l'ho trattata come CHI-QUADRO.
Si standardizzano le variabili per ottenere una N(0,1) utilizzando la formula (x-mu)/sigma. Per CHI-QUADRO si eleva al quadrato.
Si imposta quindi T=X/sqrt(Y/n) |