| Autore |
 Discussione Discussione  |
|
Domenicodattoma
Utente medio
 

Prov.: Bari
Città: Conversano

|
 Inserito il - 04/02/2010 : 12:46:48 Inserito il - 04/02/2010 : 12:46:48




|
|
Ragazzi vorrei sapere come si riconosce un reticolo dstributivo? Il riconoscimento è grafico o si effettuano delle operazioni? Grazie mille!
|
E' impossibile sapere tutto. E' però possibile sapere sempre dove poter recuperare ogni genere di informazione. |
|
|
Mark81
Utente giovane

Regione: Puglia
Prov.: Bari
Città: Adelfia

|
 Inserito il - 04/02/2010 : 13:00:47 Inserito il - 04/02/2010 : 13:00:47




|
Ciao,
ci sono vari modi per vedere se un reticolo è distributivo:
potresti usare la caratterizzazione:
un reticolo è distributivo se e solo se non contiene sottoreticoli nè di tipo M3 (diamante o trirettangolo) nè di tipo N5 (pentagono).
oppure puoi utilizzare la definizione:
un reticolo è distributivo se:
1) per ogni x,y,z appartenenti ad A x^(y v z)= (x^y) v (x^z)
2) per ogni x,y,z appartenenti ad A x v (y ^ z)= (x v y) ^ (x v z)
ovvero dei provare che il reticolo gode della proprietà distributiva (sia dell'intersezione rispetto all'unione, si dell'unione rispetto all'intersezione). Se esistono almeno 3 elementi che non verificano la 1 o la 2 il reticolo non è distributivo.
o ancora
se il reticolo è tot. ordinato allora è distributivo...
poi ci sono esempi significativi come:
- per ogni n>=2 (Dn,|) è distributivo
- il reticolo delle parti di un insieme X è distributivo
Insomma ci sono diversi modi, sia grafici che teorici, per verificare la distributività di un reticolo. |
Marco |
 |
|
|
Gogeta SSJ4
Utente medio
 

|
 Inserito il - 04/02/2010 : 13:13:47 Inserito il - 04/02/2010 : 13:13:47




|
| Il metodo piu semplice ed intuitivo però è quello secondo il quale verifichi prima i complementi dei vari elementi del reticolo. Se vi sono elementi con piu di un complemento allora sicuramente non è distributivo. I due metodi piu veloci sono questo da me citato e quello di individuare un eventuale sottoreticolo di tipo M3 o N5. |
 |
|
|
Domenicodattoma
Utente medio
 

Prov.: Bari
Città: Conversano

|
 Inserito il - 04/02/2010 : 13:43:43 Inserito il - 04/02/2010 : 13:43:43




|
Innanzitutto grazie ad entrambi per le vostre risposte...
Una cosa sola non so: cosa significa reticolo di tipo M3 oppure N5?
grazie ancora per l'aiuto! |
E' impossibile sapere tutto. E' però possibile sapere sempre dove poter recuperare ogni genere di informazione. |
 |
|
|
Gogeta SSJ4
Utente medio
 

|
 Inserito il - 04/02/2010 : 16:35:59 Inserito il - 04/02/2010 : 16:35:59




|


Il primo è il reticolo M3, il secondo il reticolo N5. Il primo si chiama trirettangolo o diamante e la distributività nn si verifica fra i 3 elementi non confrontabili ovvero a,b,c. Il secondo si chiama pentagono e anche qui la distributività nn si verifica fra i 3 elementi non confrontabili a,b,c. Non confrontabili significa che non sono in relazione fra loro. |
 |
|
|
Domenicodattoma
Utente medio
 

Prov.: Bari
Città: Conversano

|
 Inserito il - 04/02/2010 : 17:36:59 Inserito il - 04/02/2010 : 17:36:59




|
| Perfetto grazie mille! |
E' impossibile sapere tutto. E' però possibile sapere sempre dove poter recuperare ogni genere di informazione. |
 |
|
|
Domenicodattoma
Utente medio
 

Prov.: Bari
Città: Conversano

|
 Inserito il - 05/02/2010 : 14:21:48 Inserito il - 05/02/2010 : 14:21:48




|
| Vorrei chiedere una cosa a Gogeta...ho trovato un esercizio che dà A={1,3,4,6,8,24} e considera il reticolo (A,|). Dal diagramma di Hasse sembra che ci siano elementi con più complementi (4 ha 3 e 6 come complemento)...ma il reticolo sembra distributivo. Come si spiega questa cosa? Ho forse sbagliato io qualche considerazione? |
E' impossibile sapere tutto. E' però possibile sapere sempre dove poter recuperare ogni genere di informazione. |
 |
|
|
Gogeta SSJ4
Utente medio
 

|
 Inserito il - 05/02/2010 : 15:14:57 Inserito il - 05/02/2010 : 15:14:57




|
| Se provi a prendere 3 elementi fra quelli non confrontabili tipo 3,4,8 e applicare la proprietà distributiva, ovvero 4 unito (3 intersezione 8) e verifichi che valori hai da entrambi gli insiemi vedrai che ottieni due valori diversi per cui non è distributivo, anche se dalla figura non si individuano sottoreticoli di tipo M3 o N5. Questo perchè se individui un sottoreticolo di tipo M3 o N5 sai subito che nn è distributivo, però se non ci sono non è detto che sia distrubutivo per questo devi verificare i complementi dei vari elementi. |
 |
|
|
bantux87
Utente medio
 

|
 Inserito il - 05/02/2010 : 17:34:02 Inserito il - 05/02/2010 : 17:34:02




|
| il reticolo non è distributivo..come diceva gogeta nn vale una delle due proprietà distributive..xò la prof disse un reticolo non distributivo contiene necessariamente un sottoreticolo di tipo M3 o N5..che ineffetti sembra nn esserci..perkè se togli il 6 dall'insieme hai che mcm(3,4)=12 ke nn appartiene all'insieme ke ci hai dato..se togli invece il 3 il MCD(6,8)=2 che nn appartiene all'insieme..nn si riesce a far valere la chiusura..sicuro ke è quello l'insieme?è strano.. |
 |
|
|
Domenicodattoma
Utente medio
 

Prov.: Bari
Città: Conversano

|
 Inserito il - 05/02/2010 : 18:21:25 Inserito il - 05/02/2010 : 18:21:25




|
Si si, l'insieme è quello, e in effetti Gogeta ha ragione...evidentemente la prof si sarà sbagliata...comunque trovo più comodo farlo con la regola dei complementi...speriamo bene! :D
Grazie ad entrambi per l'aiuto!!!! |
E' impossibile sapere tutto. E' però possibile sapere sempre dove poter recuperare ogni genere di informazione. |
 |
|
|
bantux87
Utente medio
 

|
 Inserito il - 05/02/2010 : 18:46:03 Inserito il - 05/02/2010 : 18:46:03




|
| si vedendo i complementi nn perdi tempo a cercare sottoreticoli a meno ke non te lo kieda la traccia..ma di solito nn dovrebbe kiederlo |
 |
|
|
rem
Nuovo Utente

|
 Inserito il - 13/06/2011 : 20:39:29 Inserito il - 13/06/2011 : 20:39:29



|
| ragazzi come faccio a mostrare che i reticoli N5 e M3 non sono distributivi? |
 |
|
|
batonin
Utente medio
 

|
 Inserito il - 10/10/2012 : 11:08:24 Inserito il - 10/10/2012 : 11:08:24




|
Ragazzi, sareste cosi gentili da spiegarmi in che modo si uniscono i punti di un diagramma di Hasse?
Ad esempio, ho A={n€N | n divide sia 210 che 140}. Mi trovo il MCD(210,140)= 70 e quindi considero un nuovo insieme composto dai divisori di 70: questo insieme sarà quindi A={1,2,5,7,10,14,35,70}.
Giusto?
Ovviamente gli apici del diagramma di Hasse saranno 1 e 70, rispettivamente minimo e massimo. Ma gli altri punti in che modo li unisco? Cioe, con quale ragionamento?
Grazie mille a tutti coloro che vorranno aiutarmi, buona giornata. |
 |
|
|
Stewie83
Utente medio
 

Prov.: Brindisi
Città: Brindisi

|
 Inserito il - 14/10/2012 : 19:29:57 Inserito il - 14/10/2012 : 19:29:57




|
facilissimooo
Immagine:
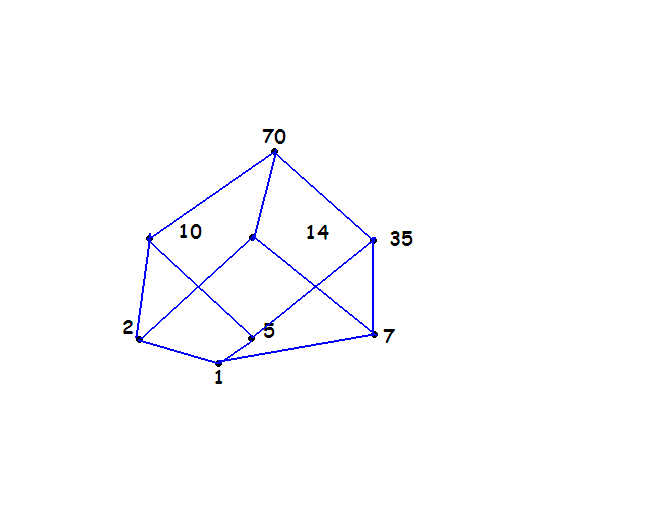
11,71 KB |
********a volte è meglio stare in silenzio e passare per deficienti che parlare e dare conferma************************************************ |
 |
|
|
batonin
Utente medio
 

|
 Inserito il - 16/10/2012 : 12:40:53 Inserito il - 16/10/2012 : 12:40:53




|
Grazie mille Stewie83 per aver inserito l'immagine, hai chiarito i miei dubbi: grazie mille!!! ;-)
Saresti cosi gentile da rispondere alle domande presenti sulla traccia di questo esercizio, in modo da farmi capire definitivamente come si ragiona sui reticoli? Magari anche spiegando brevemente come si ragiona...
Le domande sono le seguenti:
a) determinare, se esistono, i complementi di ciascun elemento
b) stabilire se si tratta di un reticolo di Boole
c) verificare se il reticolo dei divisori di 14 è un suo sottoreticolo.
Io ho le seguenti definizioni ma non riesco ad applicarle all'esercizio in questione:
Complemento: se in un reticolo limitato (cioè ammette minimo e massimo) esiste x’ in A t.c.: (x ^ x’=0) ^ (x v x’=1).
Reticolo di Boole: quando un reticolo è distributivo e complementato (quindi anche limitato).
Sottoreticolo: quando, per ogni x,y € B, sia l’estremo inferiore di {x, y} sia l’estremo superiore di {x, y} appartengono a B (con (A, #8804;) un reticolo e B sottoinsieme di A).
Distributivo: Consideriamo un reticolo (A, #8804;) esso si dirà DISTRIBUTIVO se sono verificate le proprietà per ogni x,y,z € A:
1) x v (y ^ z) #8804; (x v y) ^ (x v z)
2) x ^ (y v z) #8805; (x ^ y) v (x ^ z)
|
 |
|
|
Stewie83
Utente medio
 

Prov.: Brindisi
Città: Brindisi

|
 Inserito il - 16/10/2012 : 21:44:39 Inserito il - 16/10/2012 : 21:44:39




|
Noto a priori che hai troppe lacune in merito a Discreta.....
Inizio per dirti che se hai preso bene appunti....e te lo sta dicendo uno che ancora deve sostenere questo esame non per ignoranza ma perchè non ha mai voglia di studiare....devi fare attenzione ai minimi particolari senza scrivere le cose come sono scritti negli appunti.....
Al momento non ho nessun appunti sotto mano...causa prestito.....cmq....se non ricordo male e ti rinfresco le idee....i complementi di un elemento di un reticolo è di una banalità ancor più banale del disegno.....Tralasciando questa premessa...ti dico già che il grafico diventa la soluzione di qualunque quesito...
Se noti bene...dal mio grafico capirai che i vari complementi sono questi:
2-35
5-14
7-10
1-70 (banalmente)
Tradotto in formule
1) (x ^ x’=0) ------------>MCD
2)(x v x’=1). ------------>mcm
Se rileggi i tuoi appunti....la 1) e la 2) non sono altro che MCD(x1,x2)=1 mcm(x1,x2)=70
MCD(2,35)=1 ^ mcm(2,35)=70
MCD(5,14)=1 ^ mcm(5,14)=70
MCD(7,10)=1 ^ mcm(7,10)=70
MCD(1,70)=1 ^ mcm(1,70)=70
Anche gli altri quesiti sono di una facilità mostruosa....ma te li lascio per compitino.... |
********a volte è meglio stare in silenzio e passare per deficienti che parlare e dare conferma************************************************ |
 |
|
|
batonin
Utente medio
 

|
 Inserito il - 17/10/2012 : 12:48:36 Inserito il - 17/10/2012 : 12:48:36




|
Grazie ancora stewie, ora dovrebbe essere tutto chiaro ;-)
Se non erro quindi, il reticolo non è di Boole perchè non è complementato (non tutti gli elementi hanno un complemento) e il reticolo dei divisori di 14 è un sottoreticolo (è la base del cubo dell'immagine): giusto?
Grazie ancora per la pazienza e disponibilità, buona giornata. |
 |
|
|
batonin
Utente medio
 

|
 Inserito il - 17/10/2012 : 17:17:38 Inserito il - 17/10/2012 : 17:17:38




|
Stewie, un ultimo aiuto per favore....Credo di aver capito i reticoli quando sono presenti numeri interi, ora il mio problema sorge davanti a tracce con relazioni!!! Ti faccio un esempio, sperando che tu possa essere per un ulteriore volta talmente gentile da spiegarmi come si fa il diagramma di Hasse:
Sull'insieme A={a,b,c,d,e,f,g} è data la relazione d'ordine R={(x,x)|x€A} U {(a,x)|x€A} U {(x,g)|x€A} U {(c,e),(b,e),(b,f),(d,f)}
Per favore, potresti farmi capire come si fa il grafico in questo caso? Mi basterebbe anche solo il grafico...
Grazie mille ancora una volta anticipatamente, anche a nome di chi come me sta capendo i reticoli grazie al tuo aiuto ;-) |
 |
|
|
Stewie83
Utente medio
 

Prov.: Brindisi
Città: Brindisi

|
 Inserito il - 17/10/2012 : 21:11:07 Inserito il - 17/10/2012 : 21:11:07




|
allora.....
Il reticolo che ti ho mostrato è Complementato.....Tutti gli elementi hanno un complemento...
Essendo mcm e MCD commutativi....non ho scritto la forma duale degli elementi...perchè ovvia...
Per fartelo capire nuovamente...TUTTI I COMPLEMENTI sono:
1-->70
2-->35
5-->14
7-->10
10-->7
14-->5
35-->2
70-->1 |
********a volte è meglio stare in silenzio e passare per deficienti che parlare e dare conferma************************************************ |
 |
|
|
batonin
Utente medio
 

|
 Inserito il - 18/10/2012 : 08:20:18 Inserito il - 18/10/2012 : 08:20:18




|
Ah giusto stewie, hai ragione non me n'ero accorto :D
Gentilmente potresti dirmi com'è il grafico dell'ultimo mio post in modo da chiarirmi gli ultimi dubbi sui reticoli?
Sull'insieme A={a,b,c,d,e,f,g} è data la relazione d'ordine R={(x,x)|x€A} U {(a,x)|x€A} U {(x,g)|x€A} U {(c,e),(b,e),(b,f),(d,f)}
Per favore, potresti farmi capire come si fa il grafico in questo caso? Mi basterebbe anche solo il grafico...
Con questo grafico non dovrei piu darti fastidio, promesso!!!
Grazie tante ancora, buona giornata. |
 |
|
|
batonin
Utente medio
 

|
 Inserito il - 24/10/2012 : 12:22:11 Inserito il - 24/10/2012 : 12:22:11




|
| Nessuno mi aiuta :( |
 |
|
 Discussione Discussione  |
|



