| V I S U A L I Z Z A D I S C U S S I O N E |
| miss smile |
Inserito il - 25/05/2010 : 13:30:23
Sto cercando di risolvere l'esercizio 3 di questo esonero degli anni scorsi. Si tratta di un'esercizio sull'interpolazione polinomiale.
Viene data la funzione f(x)=(x - 2)^2 e due nodi x1=4, x2=6.
Ho individuato il polinomio di interpolazione:
p1(x) = y1*L1(x) + y2*L2(x) = 4((x-6)/(4-6)) + 16((x-4)/(6-4)) = -2(x-6) + 8(x-4) = 2(3x - 10)
Cosa intende per "si dia una maggiorazione dell'errore |r(x)| dove r(x)=f(x)-p1(x)"??? Lo si maggiora in che modo??? Bisogna semplicemente effettuare una sottrazione tra funzioni?? Bisogna valutare l'errore nell'intervallo [4,6]???
Ringrazio in anticipo per l'aiuto. |
| 3 U L T I M E R I S P O S T E (in alto le più recenti) |
| miss smile |
Inserito il - 29/05/2010 : 10:49:39
Citazione:
Messaggio inserito da roccodigit
f(x)-p(x) è uguale a quel che vien definito resto di lagrange...Ha citato una proposizione a riguardo!
roccodigit, scusami, ma non riesco a capire come applicare la proposizione a cui tu ti riferisci:
Immagine:
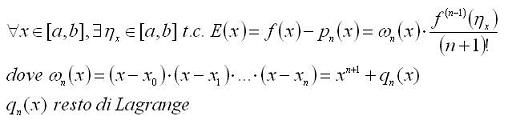
11,89 KB
|
| roccodigit |
Inserito il - 27/05/2010 : 18:20:22
nella lezione del 20 maggio ha concluso proprio con l'errore nell'interpolazione polinomiale....
f(x)-p(x) è uguale a quel che vien definito resto di lagrange...Ha citato una proposizione a riguardo! |
| miss smile |
Inserito il - 26/05/2010 : 11:38:15
...nessuno mi può aiutare?  |


![Bevuta [:273] Bevuta [:273]](http://www.laureateci.it/forum/./Immagini/../faccine/273.gif)
![compleanno [:269] compleanno [:269]](http://www.laureateci.it/forum/./Immagini/../faccine/269.gif)
![Fumata [:29] Fumata [:29]](http://www.laureateci.it/forum/./Immagini/../faccine/29.gif)
![Morte improvvisa da [:62] Morte improvvisa da [:62]](http://www.laureateci.it/forum/./Immagini/../faccine/62.gif)
![pc [:205] pc [:205]](http://www.laureateci.it/forum/./Immagini/../faccine/205.gif)
![Riproduzione [:76] Riproduzione [:76]](http://www.laureateci.it/forum/./Immagini/../faccine/76.gif)