| Autore |
 Discussione  |
|
aldo5000
Utente giovane
|
 Inserito il - 15/12/2004 : 09:38:24
|
Cmq se non mi dice che tipo di che tipo di classe deve essere posso fare cosi per semplificarmi la vita?
Poi vorrei sapere ser durante il pumping lemma vedo che la stringa pompata con i diversi casi appartiene al linguagio prendo in considerazione la stringa depompata uv^0wx^0y e continuo con la dimostrazione che stavo facendo o devo cambiare anche la dimostrazione????
Grazie mille |
 |
|
|
fabbattista
utente SEMPRE giovane
Regione: Puglia
Prov.: Bari
Città: Bari
|
Inserito il - 15/12/2004 : 10:54:22
|
Se non è di classe 3, che automa ti trovi?
Si, durante il pumping lemma puoi depompare senza cambiare dimostrazione |
|
|
|
aldo5000
Utente giovane
|
Inserito il - 15/12/2004 : 13:26:50
|
Grazie mille!
QUindi se depompo e non cambio dimostrazione automaticamente la stringa trovata non appartiene al linguaggio! E quindi non è libero da contesto il linguggio! Giusto? |
|
|
|
aldo5000
Utente giovane
|
Inserito il - 15/12/2004 : 13:28:06
|
| Ma se mi chiede di dimostrare che un linguaggio non è lineare destro posso fare la dimostrazione con lìoperazione di chiusura? E come mi faccio a stabilire quale è l1 e l2? Grazie mille dinuovo |
|
|
|
fabbattista
utente SEMPRE giovane
Regione: Puglia
Prov.: Bari
Città: Bari
|
Inserito il - 15/12/2004 : 14:56:17
|
Citazione:
Messaggio inserito da aldo5000
Grazie mille!
QUindi se depompo e non cambio dimostrazione automaticamente la stringa trovata non appartiene al linguaggio! E quindi non è libero da contesto il linguggio! Giusto?
Giusto |
|
|
|
fabbattista
utente SEMPRE giovane
Regione: Puglia
Prov.: Bari
Città: Bari
|
Inserito il - 15/12/2004 : 14:59:06
|
Citazione:
Messaggio inserito da aldo5000
Ma se mi chiede di dimostrare che un linguaggio non è lineare destro posso fare la dimostrazione con lìoperazione di chiusura? E come mi faccio a stabilire quale è l1 e l2? Grazie mille dinuovo
In genere no....
Conviene usare il pumping lemma per i linguaggi regolari |
|
|
|
aldo5000
Utente giovane
|
Inserito il - 15/12/2004 : 17:30:26
|
Scusi professore un'ultima domanda!
1. Se mi chiede una traccia di mostrare che un linguaggio tipo : L = {a^n b^2n | n > 0 } è libero ma non regolare vabbe con le operazioni di chiusura dimostro che è libero scomponendo il linguaggio e poi applico il pumping lemma per dimostrare che non è regolare. Giusto?
2. Se mi dice: Dire se L= { a^bc^k | n > 0, k > 0} è regolare, come faccio?
3. L = {a^n b^2n | n > 0 } è libero ma non lineare destro mi comporto sempre come al primo punto giusto?
4. se invece mi chiede di dimostrare se un linguaggio è lineare destro come faccio!? Apparte trovare la grammatica?
Grazie professore per l'attenzione
|
|
|
|
aldo5000
Utente giovane
|
Inserito il - 15/12/2004 : 17:42:51
|
| Professore scusate ma non contestuale che significa? |
|
|
|
alucard
Nuovo Utente
Regione: Puglia
Prov.: Foggia
Città: Margherita di Savoia
|
Inserito il - 15/12/2004 : 20:58:22
|
| Prima di fare le domande ti conviene leggere 1 po il libro...c'è scritto tutto!Non contestuale significa LIBERO DA CONTESTO!ciauz |
Si Fa Quel Ke Si Può! |
|
|
|
aldo5000
Utente giovane
|
Inserito il - 15/12/2004 : 23:54:11
|
Si ok prof ma il libro è un po ambiguo
vorrei solo delle conferme no solo le dimostrazioni
1. Se mi chiede una traccia di mostrare che un linguaggio tipo : L = {a^n b^2n | n > 0 } è libero ma non regolare vabbe con le operazioni di chiusura dimostro che è libero scomponendo il linguaggio e poi applico il pumping lemma per dimostrare che non è regolare. Giusto?
2. Se mi dice: Dire se L= { a^bc^k | n > 0, k > 0} è regolare, come faccio?
3. L = {a^n b^2n | n > 0 } è libero ma non lineare destro mi comporto sempre come al primo punto giusto?
4. se invece mi chiede di dimostrare se un linguaggio è lineare destro come faccio!? Apparte trovare la grammatica?
Grazie professore per l'attenzione |
|
|
|
fabbattista
utente SEMPRE giovane
Regione: Puglia
Prov.: Bari
Città: Bari
|
Inserito il - 16/12/2004 : 13:15:45
|
Citazione:
Messaggio inserito da aldo5000
Scusi professore un'ultima domanda!
1. Se mi chiede una traccia di mostrare che un linguaggio tipo : L = {a^n b^2n | n > 0 } è libero ma non regolare vabbe con le operazioni di chiusura dimostro che è libero scomponendo il linguaggio e poi applico il pumping lemma per dimostrare che non è regolare. Giusto?
NO. In questo caso la proprietà di kiusura non si applica perke' se scomponi il linguaggio nei due linguaggi a^n e b^2n ottieni ke i due linguaggi sono regolari e lo è anke la loro concatenazione. Questo esercizio si dimostra con il pumping lemma per i regolari (ke ti dimostra ke non è regolare). Poi trovi la grammatica libera da contesto ke genera L e hai finito
Citazione:
2. Se mi dice: Dire se L= { a^bc^k | n > 0, k > 0} è regolare, come faccio?
Trrova una espressione regolare, o un automa o un agrammatica lineare destra (ke per il teroema di kleen sono equivalenti)
Citazione:
3. L = {a^n b^2n | n > 0 } è libero ma non lineare destro mi comporto sempre come al primo punto giusto?
[/quot]
Si
[quote]
4. se invece mi chiede di dimostrare se un linguaggio è lineare destro come faccio!? Apparte trovare la grammatica?
Come per il punto 2
|
|
|
|
fabbattista
utente SEMPRE giovane
Regione: Puglia
Prov.: Bari
Città: Bari
|
Inserito il - 16/12/2004 : 13:17:10
|
Citazione:
Messaggio inserito da aldo5000
Si ok prof ma il libro è un po ambiguo
Alucard non sono io, comunque è giusto ke tu dia una lettura attenta al libro
|
|
|
|
xlinux
Nuovo Utente
|
Inserito il - 16/12/2004 : 14:14:18
|
Sapete se sono usciti i risultati di linguaggi del corso A?
Grazie! |
|
|
|
Xadier Kerloft
Nuovo Utente
Regione: Puglia
|
Inserito il - 16/12/2004 : 17:14:45
|
| Qualcuno sa se i risultati saranno postati qui entro stasera? |
DDP |
|
|
|
aldo5000
Utente giovane
|
Inserito il - 16/12/2004 : 17:32:55
|
Salve professore,
grazie mille per l'aiuto che mi sta dando!
Vorrei solo una conferma!
Devo dimostrare che un L={1^n2^(2n)|n>0} non è lineare destro!
Come mi ha detto in precedenza per l'equivalenza della classe dei linguaggi applico il pumping lemma per i linguaggi regolari
Ora la stringa che prendo in cosiderazione puo essere:
1. a^n e dimostro che l'automa che riconosce le a ha un ciclo j-i e che quindi riconosce un numero di a pari a^(n+k(j-i)) che non appartiene al linguaggio. Sempre qui posso anche dire dire che l'automa riconosce a^jb^(2i) che cmq non appartiene al linguaggio! Quindi non è regolare
2. posso considerare b^(2n)? dicendo che l'automa legge le prime n a poi si sposta alle b ecc. come al punto primo.
|
|
|
|
fel
Nuovo Utente
Prov.: Bari
|
Inserito il - 05/01/2005 : 12:03:33
|
salve professore.vorrei farle una domanda...dovend dimostrare se un liguaggio è libero da contesto, come faccio a riconoscere ke tipo di pumping lemma devo utilizzare??
cioè applicando il puming lemma per i linguaggi regolari, devo utilizzare il metodo per il quale distinguo i vari casi oppure confronto la lunghezza della stringa pompata kon quella successiva??
la ringrazio |
|
|
|
fabbattista
utente SEMPRE giovane
Regione: Puglia
Prov.: Bari
Città: Bari
|
Inserito il - 06/01/2005 : 00:11:37
|
| fel se leggi le pagine precedenti dovresti trovare la risposta. Comunque dipende dalle caratteristiche del linguaggio (i vincoli esistenti nella definizione)..... |
|
|
|
dr.Wolf
Utente medio
Regione: Puglia
Prov.: Lecce
Città: Arnesano
|
Inserito il - 06/01/2005 : 10:10:06
|
salve prof, sono uno studente del corso A ,saprebbe
per cortesia quale è stata la traccia di laboratorio
del 13 Dicembre? Non riesco a trovarla su valis
|
CAMPIONI!!! |
|
|
|
fabbattista
utente SEMPRE giovane
Regione: Puglia
Prov.: Bari
Città: Bari
|
Inserito il - 06/01/2005 : 11:12:37
|
Citazione:
Messaggio inserito da Liga84
salve prof, sono uno studente del corso A ,saprebbe
per cortesia quale è stata la traccia di laboratorio
del 13 Dicembre? Non riesco a trovarla su valis
Eccola.
Implementare in linguaggio C il seguente automa, definito sull’alfabeto X = {0, 1, O, I}
Immagine:
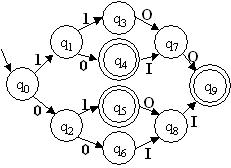
11,55 KB |
|
|
|
dr.Wolf
Utente medio
Regione: Puglia
Prov.: Lecce
Città: Arnesano
|
Inserito il - 06/01/2005 : 11:58:31
|
| Prof la ringrazio |
CAMPIONI!!! |
|
|
|
Discussione |
|
Domande per il docente del corso B
Discussione Bloccata
