| Autore |
 Discussione  |
|
|
elsandro88
Utente medio
.gif)
Regione: Puglia
Città: Bari
|
 Inserito il - 26/04/2010 : 18:47:29
|
Sia X una v.a di Poisson P(1) e Y una Bernoulli con p=1/2
determinare la funzione di probabilità Z:=X+Y
|
Cervello. Un apparato che pensa di pensare... |
|
|
elsandro88
Utente medio
Regione: Puglia
Città: Bari
|
Inserito il - 26/04/2010 : 19:08:52
|
| qualcuno l'ha risolto? |
Cervello. Un apparato che pensa di pensare... |
 |
|
|
The_Mad_Hatter
Utente medio
|
Inserito il - 26/04/2010 : 19:23:51
|
Allora... innanzitutto notiamo che Z assume valori {0, 1, 2, ....}
Poi vediamo che:
X | Y | Z
-----------
0 | 0 | 0 P({X=0} intersez. {Y=0})
0 | 1 | 1 P({X=0} intersez. {Y=1})
1 | 0 | 1 P({X=1} intersez. {Y=0})
1 | 1 | 2 P({X=1} intersez. {Y=1})
2 | 0 | 2 P({X=2} intersez. {Y=0})
2 | 1 | 3 ....
3 | 0 | 3
3 | 1 | 4
Quindi, supponendo che X e Y siano indipendenti, abbiamo:
Pz(0) = P(Z=0) = P(X=0) P(Y=0) = (1-p) * e^(-lambda) = 1/2e
Per k>0:
Pz(k) = P(X=k-1) P(Y=1) + P(X=k) P(Y=0) =
= ( lambda^(k-1) / (k-1)! ) * e^(-lambda) * p + ( lambda^k / k! ) * e^(-lambda) * (1-p) =
= ( lambda^(k-1) / (k-1)! ) * e^(-lambda) * (p + (lambda/k)*(1-p)) =
= ( 1^(k-1) / (k-1)! ) * e^(-1) * ( 1/2 + (1/k)*(1/2)) =
= (1/2) * (1/(k-1)!) * e^(-1) * (1 + 1/k)
...ci vorrebbe un modo nel forum per convertire le formule testuali in linguaggio matematico.. queste scritte così sono praticamente illeggibili!
EDIT:
In allegato, un'immagine chiarificatrice!
Immagine:
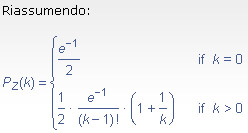
25,15 KB |
Modificato da - The_Mad_Hatter in data 26/04/2010 19:34:08 |
|
|
|
Mk178
Moderatore ITPS
Regione: Puglia
Prov.: Bari
|
Inserito il - 26/04/2010 : 21:42:07
|
| e da dove esce questo esercizio??? |
PER ESSERE SEMPRE AGGIORNATI
Sottoscriviti alla discussione ITPS/Generale/INFORMAZIONI
(NON postate in questo topic le vostre richieste)
Oppure Iscriviti al gruppo su Facebook Informatica T.P.S. Bari
EX-Rappresentante LINK - udu: C. Facoltà di Scienze MM.FF.NN. & C. Corso di Laurea di Informatica TPS
|
|
|
|
elsandro88
Utente medio
Regione: Puglia
Città: Bari
|
Inserito il - 27/04/2010 : 08:55:54
|
| vecchio appello del 2007 credo |
Cervello. Un apparato che pensa di pensare... |
|
|
|
cucciola
Utente medio
Regione: Puglia
Prov.: Bari
Città: Giovinazzo
|
Inserito il - 27/04/2010 : 09:06:58
|
| ma se z:=x+y perchè ad esempio la Pz(0)=Px(0) * Py(0) ? |
zao raga
zinzia |
|
|
|
The_Mad_Hatter
Utente medio
|
Inserito il - 27/04/2010 : 10:55:10
|
Citazione:
Messaggio inserito da cucciola
ma se z:=x+y perchè ad esempio la Pz(0)=Px(0) * Py(0) ?
Perché entrambe devono essere zero, altrimenti la loro somma sarebbe diversa da zero.
Dire X=0 AND Y=0 si traduce a livello insiemistico come X=0 intersecato Y=0, e poi sfruttando l'indipendenza riusciamo a scrivere la probabilità di Z come prodotto tra le due.
E' facile convincersi che non potrebbe essere altrimenti!
Infatti, se fosse Pz(0) = Px(0) U Py(0) potremmo avere ad esempio X=2 e Y=0 (e quindi Z=2) oppure X=0 e Y=1 (quindi Z=1). |
|
|
|
The_Mad_Hatter
Utente medio
|
Inserito il - 27/04/2010 : 11:05:00
|
Citazione:
Messaggio inserito da cucciola
in tutti i miei appunti (anche quelli della mininni) l'unione si traduce in somma e l'intersezione in prodotto quindi continuo a non trovarmi!
Beh, allora lo vedi che dovresti trovarti? :)
Infatti, la probabilità che Z sia 0, ovvero la probabilità xhe X+Y=0 è esattamente la probabilità dell'intersezione tra gli eventi X=0 e Y=0.
Quindi si traduce, come sempre, in un prodotto e non in una somma! |
|
|
|
cucciola
Utente medio
Regione: Puglia
Prov.: Bari
Città: Giovinazzo
|
Inserito il - 27/04/2010 : 11:13:32
|
| ah ok ora ho capito! non riuscivo a capire come dovesse essere la tabella scritta sopra da The_Mad_Hatter e non mi trovavo! |
zao raga
zinzia |
|
|
| |
Discussione |
|
esercizio nuovo
